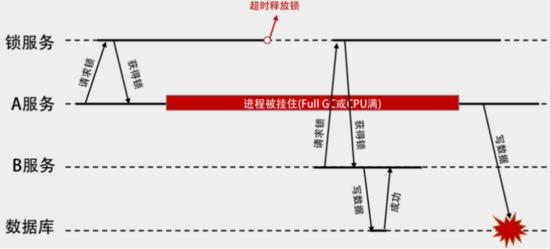
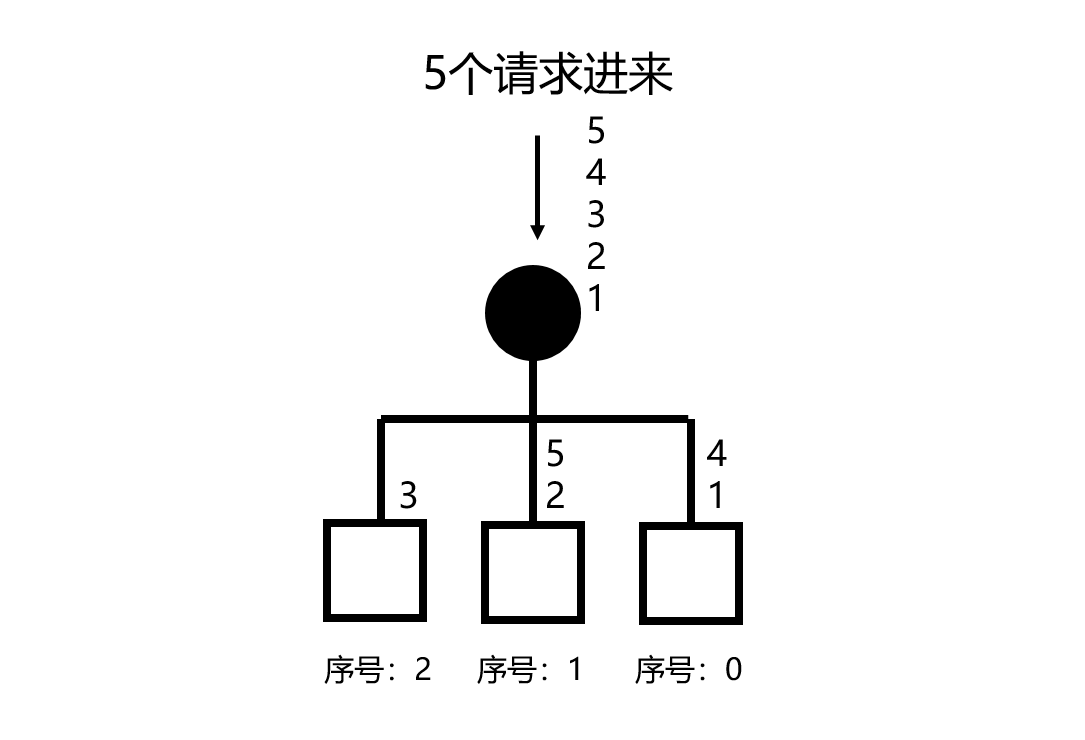
小编给大家分享一下Dijkstra算法算法最短路径的示例分析,相信大部分人都还不怎么了解,因此分享这篇文章给大家参考一下,希望大家阅读完这篇文章后大有收获、下面让我们一起去了解一下吧!
<强>某个源点到其余各顶点的最短路径
这个算法最开始心里怕怕的,不知道为什么,花了好长时间弄懂了,也写了一遍,又遇到时还是出错了,今天再次写它,心里没那么怕了,耐心研究,懂了之后会好开心的,哈哈
<强> Dijkstra算法算法:

如图克图:若要求从顶点1到其余各顶点的最短路径,该咋求;
迪杰斯特拉提出“按最短路径长度递增的次序”产生最短路径。
首先,在所有的这些最短路径中,长度最短的这条路径必定只有一条弧,且它的权值是从源点出发的所有弧上权的最小值,例如:在图G中,从源点1出发有3条弧,其中以弧(1、2)的权值为最小,因此,(1,2)不仅是1到2的一条最短路径,并且它可能是源点到其它各个终点的最短路径中的一条子路径。
其次,第二条长度次短的最短路径只可能有两种情况:①它或者只含一条从源点出发的弧且弧上的权值大于已求得最短路径的那条弧的权值,但小于其他从源点出发的弧上的权值②它或者是一条只经过已求得最短路径的顶点的路径。
例如图G中,从1到其他各点。过程中,用d[我]保存从1到我的的最短路径(过程会变化),初值为:若源点到该源点有弧,则为权值,否则初始化为无穷大,每求得一条到达某个终点我的最短路径,就继续检查是否存在以此路径为子路径的到达其他点的最短路径,若存在,判断其长度是否比当前求得的路径长度短,若短,就更新为更短的长度。
如图G中,求得到2的最短路径d[2]为10,就把d[2]作为与两相连的到其他点的子路径继续检查,得到到3的最短路径为d [2] + 50=60
<>强过程:
(1)。令S={1},年代集合中表示已经找到最短路径的结点,开始时1为源点,并设定d[我]的初始值为:d[我]=(我),
(2)。求出到j点的最短路径,j点为不在年代集合中的某点
d [j]=分钟{d[我]}
(3)。判断所有没在年代集合中的顶点k,若d [k]在d [j] + (j, k)则修改d [k]的值为:
d [k]=d [j] + (j, k)
(4)。重复(2)。(3)操作共n - 1次,每次操作,在(2)得到一个到
某点的最短路径。
<强>有向图求最短路径
<强>无向图求最短路径
无向图也是相同思路:在构造邻接矩阵时考虑对称就行。
<强>无向图求最短路径且有路径输出
在求最短路的过程中,最短路①它或者是从源点出发的弧②它或者是一条经过已到其他最短路径的顶点的路径。