基于Python共轭梯度法与最速下降法之间的对比 - 行业资讯

在一般问题的优化中,最速下降法和共轭梯度法都是非常有用的经典方法,但最速下降法往往以“之”字形下降,速度较慢,不能很快的达到最优值,共轭梯度法则优于最速下降法,在前面的某个文章中,我们给出了牛顿法和最速下降法的比较,牛顿法需要初值点在最优点附近,条件较为苛刻。

算法《数值最优化方法》高立,P111

我们选用了64维的二次函数来作为验证函数,具体参见上书111页。

<强>共轭梯度方法(FR格式),共轭梯度法(PRP格式),最速下降法

　　　　　　# - * -编码:utf - 8 - * 　　”“” 　　创建alt="基于Python共轭梯度法与最速下降法之间的对比">

从图中可以看的出,最速下降法SD的迭代次数是最多的,在与共轭梯度(FR与PRP两种方法)的比较中,明显较差。

<强> python实现牛顿迭代法和二分法求平方根,精确到小数点后无限多位4

首先来看一下牛顿迭代法求平方根的过程:计算3的平方根

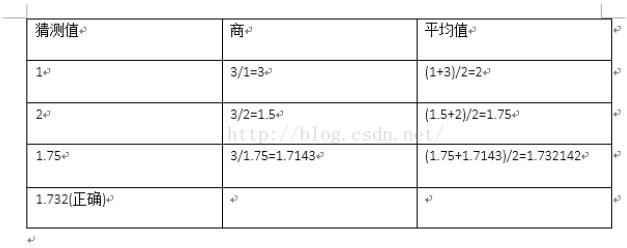
基于Python共轭梯度法与最速下降法之间的对比

如图,是求根3号的牛顿迭代法过程。这里使用的初始迭代值(也就是猜测值)为1,其实可以为任何值最终都能得到结果。每次开始,先检测猜测值是否合理,不合理时,用上面的平均值来换掉猜测值,依次继续迭代,直到猜测值合理。

<强>原理:现在取一个猜测值,如果猜测值合理的话,那么就有一个^ 2=x,即x/=a, x为被开方数。不合理的话呢,就用表中的猜测值和商的平均值来换掉猜测值。当不合理时,比如a>真实值,那么x/a<真实值,这时候取一个与x/的平均值来代替一个的话,那么新的一个就会比原来的一个要更接近真实值。同理有a<真实值的情况。于是,这样不断迭代下去最终是一个一个不断收敛到真实值的一个过程。于是不断迭代就能得到真实值,证明了迭代法是正确的。

<强>附上我的python代码:

利用python整数运算,python整数可以无限大,可以实现小数点后无限多位

#二分法求x的平方根小数点下任意K位数的精准值,利用整数运算#思想:利用二分法,每次乘以10,取中间值,比较大小,从而定位精确值的范围,将根扩大10倍,则被开方数扩大100倍。#商(商)牛顿迭代法:先猜测一个值,再求商,然后用猜测值和商的中间值代替猜测值,扩大倍数,继续进行。

　　　　　　　　　　导入数学　　从数学进口√6 　　　　def check_precision (l、h p, len1): #检查是否达到了精确位　　l=str (l); h=str (h) 　　如果len (l) & lt;=len1 + p或者len (h) & lt;=len1 + p: 　　返回假　　因为我在范围(len1 p + len1): #检查小数点后面的p个数是否相等　　如果l(我)!=h[我]:#当l h和某一位不相等时,说明没有达到精确位　　返回假　　还真　　　　def print_result (x, len1, p): 　　x=str (x) 　　如果len (x) -len1 x: 　　h=m 　　其他: 　　l=m 　　返回print_result (l, len1, p) #当达到了要求的精度,直接返回l 　　　　#牛顿迭代法求平方根　　def newton_sqrt (x, p): 　　x0=int (sqrt (x)) 　　如果x0 * x0==x: #完全平方数直接开方,不用继续进行　　print_result (x0, len (str (x0)), p) 　　返回　　len1=len (str (x0)) #找出整数部分的长度　　g=1; q=x//g, g=(g + q)//2 　　而(不是check_precision (g, q, p, len1)): 　　x=x * 100 　　g=g * 10 　　q=x//g #求商　　g=(g + q)//2 #更新猜测值为猜测值和商的中间值　　返回print_result (g, len1, p) 　　　　而真正的: 　　x=int(输入(“请输入待开方数:")) 　　p=int(输入(“请输入精度:")) 　　打印(“binary_sqrt:“结束=" ") 　　binary_sqrt (x, p) 　　打印(“newton_sqrt:“结束=" ") 　　newton_sqrt (x, p)