使用Java怎么编写一个递归程序 - 行业资讯 - 肥雀云

　　介绍

这篇文章将为大家详细讲解有关使用Java怎么编写一个递归程序,文章内容质量较高,因此小编分享给大家做个参考,希望大家阅读完这篇文章后对相关知识有一定的了解。

递归的定义

递归(递归):以此类推是递归的基本思想,将规模大的问题转化为规模小的问题来解决。

递归的要素

自定义递归函数,并确定函数的基本功能
例如Java从键盘输入一个数,求输入这个数的阶乘。这个时候把输入的数字作为形参

int diGuiTest (int n ) { 　　}

找到递归函数循环结束条件
在求阶乘的时候,我们不妨做出如下思考,例如输入的n是5,那么5 !是5 * 4 3 * 2 * 1,那是不是可以写成n
f (n - 1) ?,程序运行过程如下:
5 * (4)
f(4)相当于重新调用了函数,形参为4
5 * 4 * (n - 1)
f(3)相当于重新调用了函数,形参为3
5 * 4 * 3 * (n - 1)
f(2)相当于重新调用了函数,形参为2
5 * 4 * 3 * 2 * (n - 1)
f(1)相当于重新调用了函数,形参为1
很容易发现,这时候如果递归调用到n为1的时候,就要结束调用自身
代码如下:

int diGuiTest (int n ) { 　　如果(n==1) { 　　return 1; 　　} 　　其他{ 　　return n * f (n - 1); 　　} 　　}

代码示例

<强>求1 - 100之间所有自然数的和

int sum (int n ) { 　　如果(n==1) { 　　return 1,; 　　} 　　其他{ 　　return n +数目(n - 1); 　　} 　　}

<>强斐波拉契数列
斐波那契数列(斐波那契序列),又称黄金分割数列,因数学家莱昂纳多·斐波那契(莱昂纳多斐波那契)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0,1,1,2,3,5,8,13日,21日,34岁……在数学上,斐波那契数列以如下被以递推的方法定义:F (0)=0, F (1)=1, F (n)=F (n - 1) + F (n - 2) (n≥2, n∈n *)

int 斐波纳契(int n ) { 　　　　if (n<=1) { 　　return n; 　　} 　　else { 　　return 斐波纳契(n - 1) +斐波纳契(n - 2); 　　} 　　　　}

<>强汉诺塔问题

使用Java怎么编写一个递归程序”> 首先我们考虑最简单的情况: <img src=

public class Hanio { 　　public 才能;static void main (String [], args), { 　　,,,char A=& # 39;一个# 39;; 　　,,,char B=& # 39; B # 39;; 　　,,,char C=& # 39; C # 39;; 　　,,,hannio (3 A, B, C); 　　,,} 　　,,static void hannio (char int paltfrom, char ; B,, char C) { 　　,,,if (paltfrom==1) { 　　,,,,,move (A、C); 　　,,,}else { 　　,,,,,hannio (paltfrom-1, A, C, B);//上面两个盘子,通过C柱到B柱　　,,,,,move (A、C); 　　,,,,,hannio (paltfrom-1, B, C);//,,,} 　　,,} 　　,,static void 移动(char char B) { 　　,,,System.out.println (“+, - - - - -, + B); 　　,,} 　　}

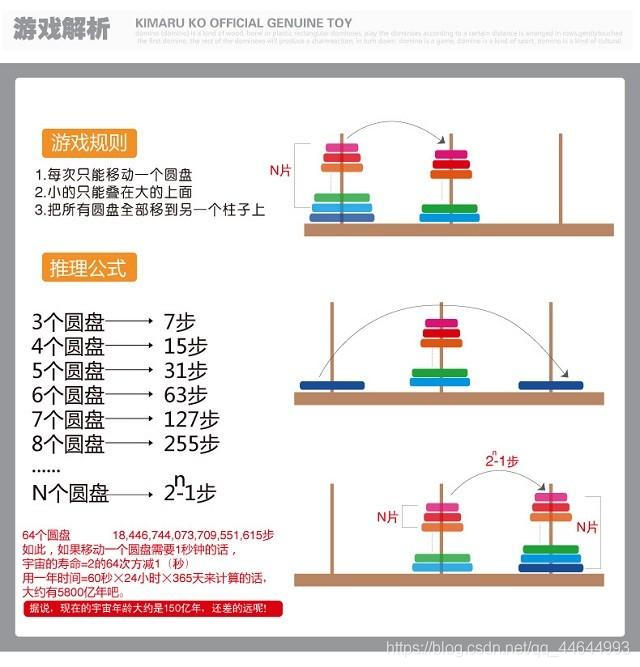
关于使用Java怎么编写一个递归程序就分享到这里了,希望以上内容可以对大家有一定的帮助,可以学到更多知识。如果觉得文章不错,可以把它分享出去让更多的人看的到。